Bayesian optimization is a powerful technique for the optimization of expensive black-box functions, but typically limited to low-dimensional problems. Here, we extend this setting to higher dimensions by learning a lower-dimensional embedding within which we optimize the black-box function.
Bayesian optimization is a powerful technique for the optimization of expensive black-box functions. It is used in a wide range of applications such as in drug and material design and training of machine learning models e.g. large deep networks. We propose to extend this approach to high-dimensional settings, that is where the number of parameters to be optimized exceeds 10-20. We do so by learning a low-dimensional nonlinear feature space of the inputs where we can optimize the black-box objective function. With our model we achieve higher compression rates with respect to linear models1 and superior data efficiency with respect to deep networks2.
Probabilistic model
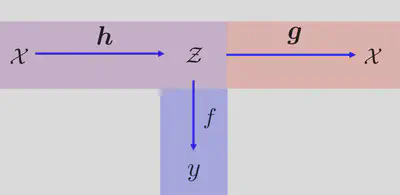
Our model jointly solves two distinct tasks: (i) a regression from feature space to observations (in blue) and (ii) a reconstruction mapping from feature space to high-dimensional space (in red). The $\boldsymbol{h}$ mapping characterizes the encoder which we define as a multilayer perceptron. We perform Bayesian optimization in this feature space $\mathcal{Z}$, that is we learn a response surface $f$ with a Gaussian process (GP) and maximize and acquisition function $\alpha(\mathbf{z})$ in $\mathcal{Z}$. Once we selected a new point in feature space we reconstruct it to the original space $\mathcal{X}$ with the $\boldsymbol{g}$ decoder mapping which we define as a multi-output GP (MOGP)3. The composition of a GP and a neural network is called Manifold GP45.
Joint training
We apply a joint training of the marginal likelihood. We train the encoder $\boldsymbol{h}$, the response surface $f$ and the decoder $\boldsymbol{g}$ jointly with the log marginal likelihood $\mathcal{L}$. The joint training has a regularization effect on the feature space which is useful for two distinct tasks: i) response surface learning and ii) input reconstruction.
Constrained acquisition maximization
One problem that arises with the MOGP decoding is that locations in feature space, which are too far away from data, will be mapped back to the MOGP prior. To prevent mapping back to the prior, we propose a maximization of the acquisition function only over $L_{2}$ balls of the low dimensional feature space data points $\mathbf{z}_{i}$. The radius of these balls is determined by the Lipschitz constant6 of the posterior mean function of the decoder MOGP
Concluding remarks
A manifold GP learns useful low-dimensional feature representations of high-dimensional data by jointly learning the response surface and a reconstruction mapping. To avoid meaningless exploration with the acquisition function, we introduce a nonlinear constraint based on Lipschitz continuity of predictions of the reconstruction mapping.
Z. Wang, M. Zoghi, F. Hutter, D. Matheson, N. De Freitas. Bayesian optimization in high dimensions via random embeddings, International Joint Conference on Artificial Intelligence. 2013. ↩︎
R. Gomez-Bombarelli, J. Wei, D. Duvenaud, J. Hernandez-Lobato, B. Sanchez-Lengeling, D. Sheberla, and J. Aguilera-Iparraguirre, T. Hirzel, R. Adams, A. Aspuru-Guzik. Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Science. 2018. ↩︎
M. Alvarez, L. Rosasco, N. Lawrence. Kernels for vector-valued functions: a review. Foundations and Trends in Machine Learning. 2011. ↩︎
R. Calandra, J. Peters, C. Rasmussen, M. Deisenroth. Manifold Gaussian processes for regression. International Joint Conference on Neural Networks. 2016. ↩︎
A. Wilson, Z. Hu, R. Salakhutdinov, E. Xing. Deep kernel learning. International Conference on Artificial Intelligence and Statistics. 2016. ↩︎
J. Gonzalez, Z. Dai, P. Hennig, N. Lawrence. Batch Bayesian optimization via local penalization. International Conference on Artificial Intelligence and Statistics. 2016. ↩︎