Probabilistic Active Meta Learning (PAML)

Meta-learning can make machine learning algorithms more data-efficient, using experience from prior tasks to learn related tasks quicker. Since some tasks will be more-or-less informative with respect to performance on any given task in a domain, an interesting question to consider is, how might a meta-learning algorithm automatically choose an informative task to learn? Here we summarise probabilistic active meta-learning (PAML): a meta-learning algorithm that uses latent task representations to rank and select informative tasks to learn next.

PAML

In our paper¹, we consider a setting where the goal is to actively explore a task domain. We assume that the meta-learning algorithm is given a set of task descriptive observations (task descriptors) to select the next task (akin to a continuous or discrete action space). For example, task descriptors might be fully or partially observed task parameterisations (e.g., weights of robot links), high-dimensional descriptors of tasks (e.g., image data of different objects for grasping), or simply a few observations from the task itself.

PAML is based on the intuition that by formalising meta-learning as a latent variable model²³, the learned task embeddings will represent task differences in a way that can be exploited to make decisions about what task to learn next. Figure 2 shows the graphical model for active meta-learning that underpins PAML.

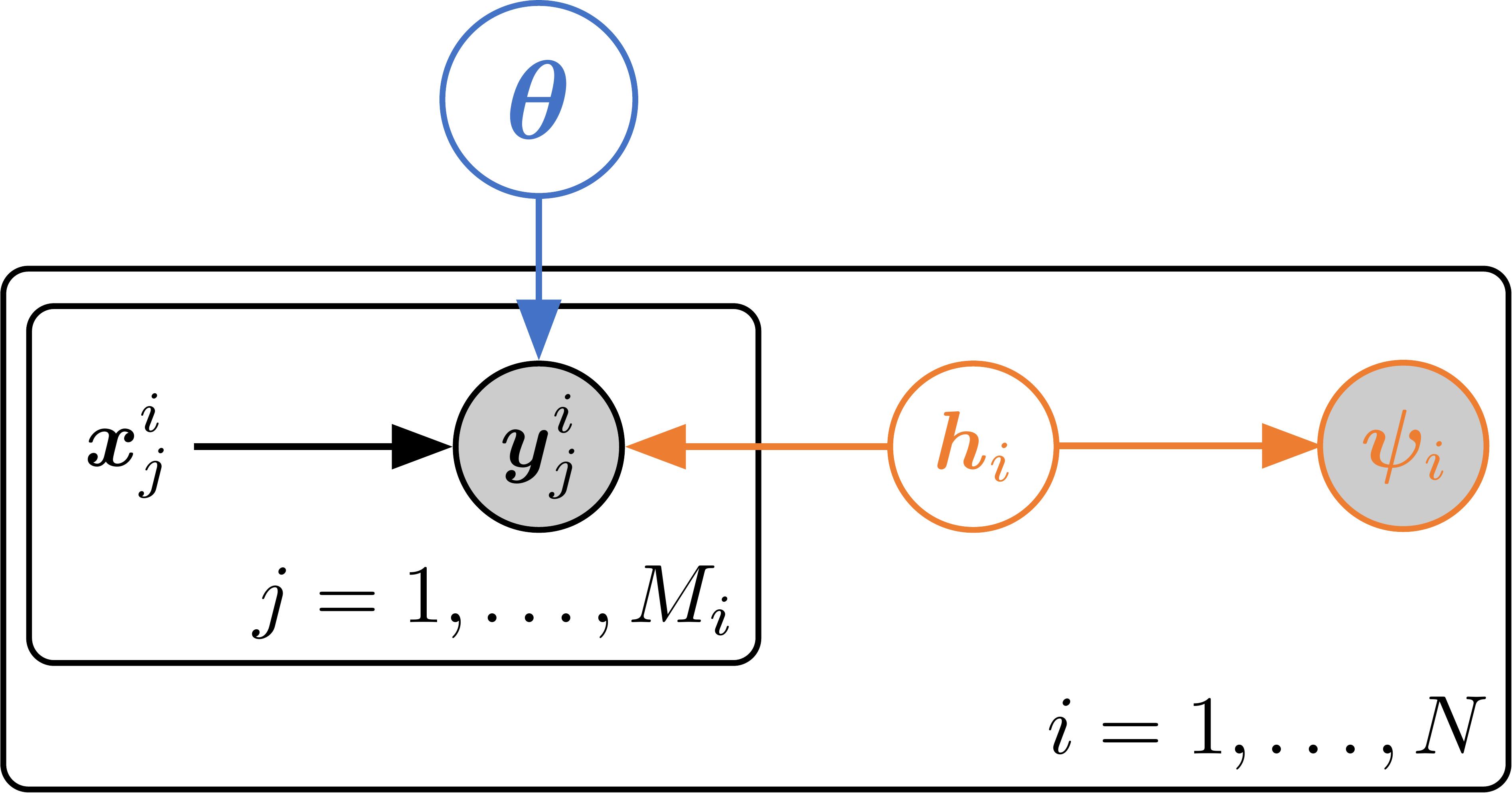
Given a set of training datasets, learning and inference is done jointly by maximising a lower on the log model evidence (ELBO), with respect to global model parameters $\theta$ and the variational parameters $\phi$ that approximate the posterior over the latent task variables $\boldsymbol{h}_i$. Since the variational posterior is chosen to be computable in closed form (e.g. Gaussian), we can naturally define a utility function as the self-information (or surprise) of a point under a mixture distribution defined by the training tasks, i.e.,

$$ u(\boldsymbol{h}^{}) := -\log \sum\nolimits_{i=1}^N q_{\phi_i}(\boldsymbol{h}^) + \log N, $$ where $N$ is the number of training tasks and $\boldsymbol{h}^*$ is the point being evaluated. The full PAML algorithm is illustrated in Figure 3.

Results

In the paper¹, we run experiments on simulated robotic systems. We test PAML’s performance on varying types of task-descriptors. We generate tasks within domains by varying configuration parameters of the simulator, such as the masses and lengths of parts of the system. We then perform experiments where the learning algorithm observes: (i) fully observed task parameters, (ii) partially observed task parameters, (iii) noisy task parameters and (iv) high-dimensional image descriptors. We compare PAML to uniform sampling (UNI), used in recent meta-learning work⁴ and equivalent to domain randomization⁵, Latin hypercube sampling (LHS) and an oracle.

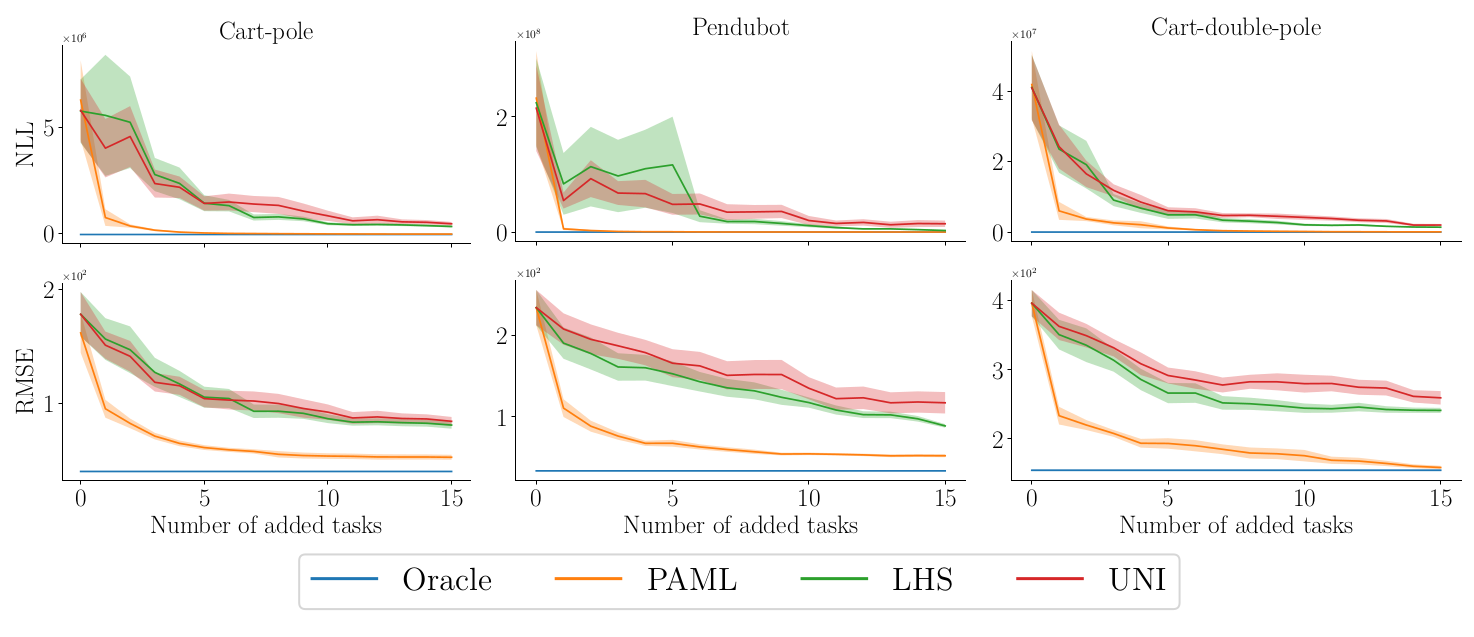
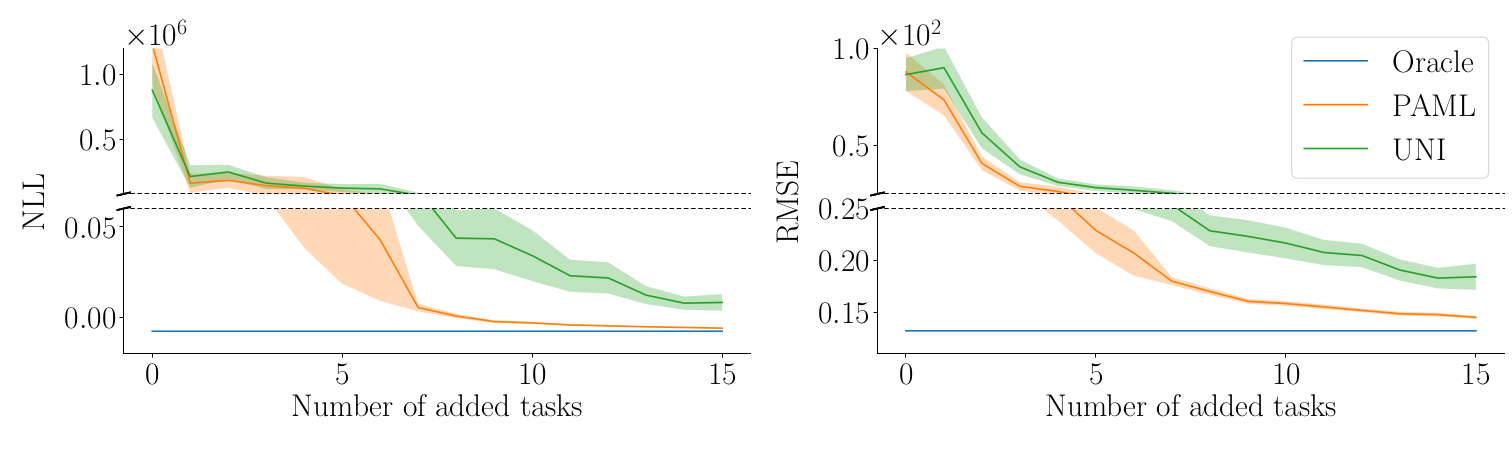
Figure 4 shows the results for observed task descriptors and Figure 5 for image task descriptors. In all experiments, we see a noticeable improvement in data-efficiency, measured as the predictive performance—i.e. RMSE and negative log-likelihood (NLL)—on a set of test tasks, plotted against the number of training tasks added.

Conclusion

To summarise, PAML is a probabilistic formulation of active meta-learning. By exploiting learned task representations and their relationship in latent space, PAML can use prior experience to select more informative tasks. The flexibility of the underlying active meta-learning model enables PAML to do this even when the task descriptors—the representation of the tasks observed by the model—are partially observed or even when they are images.

References