Research Blog

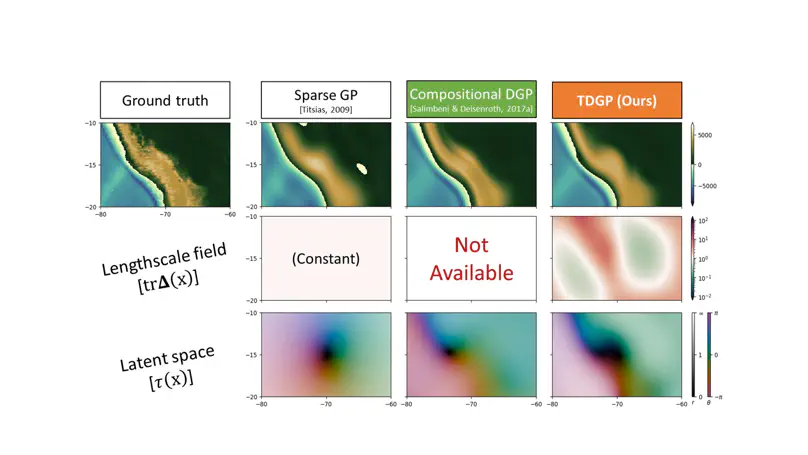
Selecting an appropriate kernel for Gaussian processes (GPs) can be challenging. Deep GPs avoid manual kernel engineering by low-dimensional embeddings of the inputs that explain the output data, but lose all the interpretability of shallow GPs. Alternatively one successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. We propose a novel synthesis of both previous approaches. Each TDGP layer is a local linear transformation generating latent embeddings while also being the lengthscales of a kernel. This model is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data and behaves well when increasing the number of layers.

Background Model-based reinforcement learning (MBRL) approaches learn a dynamics model from system interaction data and use it as a proxy of the physical system. Instead of executing actions directly on the target system, the agent queries the dynamics model, using it to generate forward trajectories of how the system will evolve given a sequence of actions.

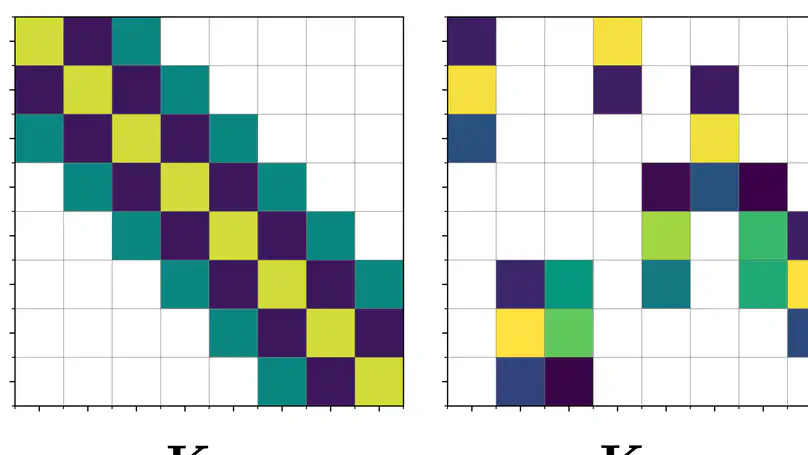
Gaussian processes infamously suffer from an $\mathcal{O}(N^3)$ computational complexity and $\mathcal{O}(N^2)$ memory requirements, rendering them intractable for even medium sized datasets where $N\gtrsim 10,000$. Sparse variational Gaussian processes have been developed to alleviate some of the pains of scaling GPs to large datasets by approximating the exact GP posterior with a variational distirbution conditioned on a small set of inducing variables designed to summarise the dataset.

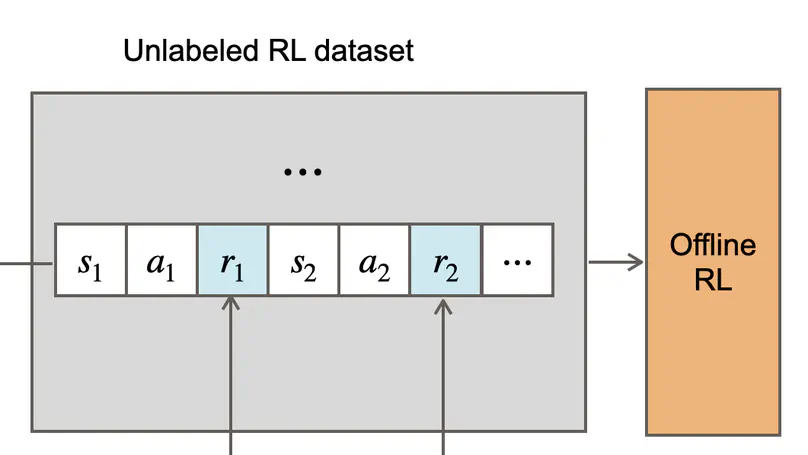
With the advent of large datasets, offline reinforcement learning (ORL) is a promising framework for learning good decision-making policies without interacting with the real environment. However, offline RL requires the dataset to be reward-annotated, which presents practical challenges when reward engineering is difficult or when obtaining reward annotations is labor-intensive.

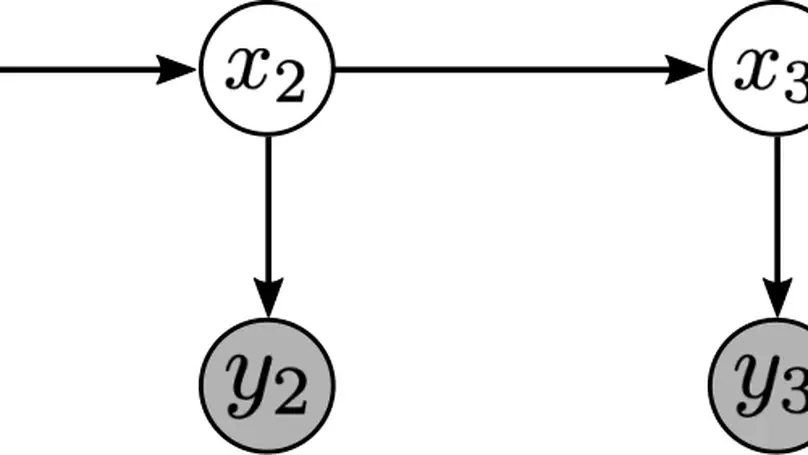
State estimation in nonlinear systems is difficult due to the non-Gaussianity of posterior state distributions. For linear systems, an exact solution is attained by running the Kalman filter/smoother. However for nonlinear systems, one typically relies on either crude Gaussian approximations by linearising the system (e.

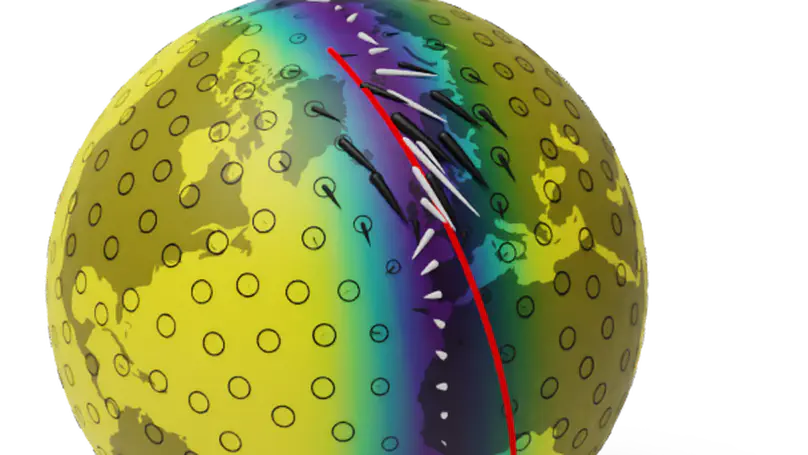
Gaussian processes are machine learning models capable of learning unknown functions with uncertainty. Motivated by a desire to deploy Gaussian processes in novel areas of science, we present a new class of Gaussian processes that model random vector fields on Riemannian manifolds that is (1) mathematically sound, (2) constructive enough for use by machine learning practitioners and (3) trainable using standard methods such as inducing points.

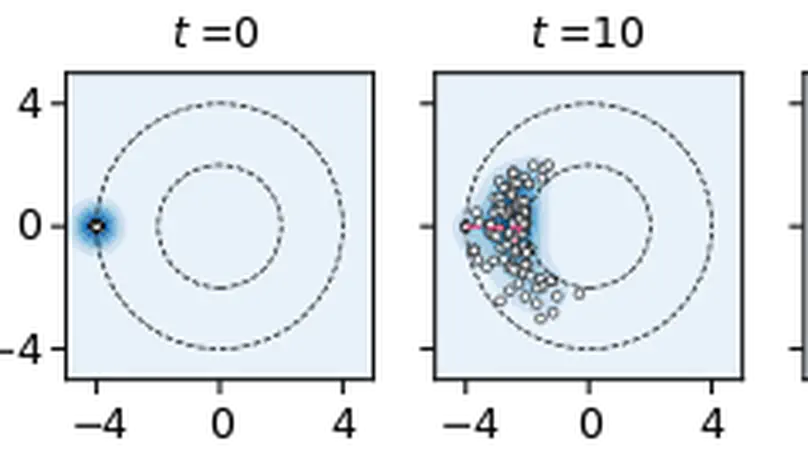
Probabilistic software analysis methods extend classic static analysis techniques to consider the effects of probabilistic uncertainty, whether explicitly embedded within the code – as in probabilistic programs – or externalized in a probabilistic input distribution.

Modeling distributions on Riemannian manifolds is a crucial component in understanding non-Euclidean data that arises, e.g., in physics and geology. We propose a class of flows that uses convex potentials from Riemannian optimal transport.

In this work, we quantify the discretisation error induced by gradient descent in two-player games, and use that to understand and improve such games, including Generative Adversarial Networks. Two-player games Many machine learning applications involve not one single model, but two models which get trained jointly.

Gaussian processes are a model class for learning unknown functions from data. They are particularly of interest in statistical decision-making systems, due to their ability to quantify and propagate uncertainty. In this work, we study analogs of the popular Matérn class where the domain of the Gaussian process is replaced by a weighted undirected graph.