Safe Trajectory Sampling in Model-based Reinforcement Learning
Background
Model-based reinforcement learning (MBRL) approaches learn a dynamics model from system interaction data and use it as a proxy of the physical system. Instead of executing actions directly on the target system, the agent queries the dynamics model, using it to generate forward trajectories of how the system will evolve given a sequence of actions. This way, the agent is able to learn a policy using minimal amounts of data and without making assumptions about the underlying dynamics of the target system. This is especially true for Gaussian process (GP) dynamics models which additionally account for the uncertainty in the state observations of the dynamical system and allow for policies which are robust to minor pertubations and measurement noise 1.
In general, the common training objective for learned dynamics models in MBRL mainly focuses on the closeness of state transitions from the learned dynamics model to those from the actual system and learning a model that accurately simulates realistic consequences (state transitions) of a given action (in the form of state trajectories). However, learned dynamics models can be blind to possible safety and feasibility constraints such as velocity limits, self-collisions, obstacle collisions, etc. Being able to satisfy these constraints is strong requirement for any policy we plan to deploy on a physical robot system. This becomes particularly problematic during the initial stages of learning when the model lacks sufficient data and produces unsafe and seemingly random trajectories. In our recent paper at CASE 2023, we successfully tackle this issue and incorporate user-defined safety constraints into the MBRL process while keeping the benefits of using a probabilistic dynamics model.
Distributional Trajectory Sampling
Assuming a Markov dynamical system with states $\mathbf{s}_t$ and actions $\mathbf{a}_t$, we can train a Gaussian process dynamics model $p(\mathbf{y} \mid \mathbf{X})$, which maps augmented states $X = [\mathbf{s}_t\, \mathbf{a}_t]$ to state differences $y = [\mathbf{s}_{t+1} - \mathbf{s}_t ]$. To make one-step predictions for next states with the GP, we sample $\mathbf{y}^*$ from the GP posterior moments $$ \begin{align} \boldsymbol{\mu}^* &= k(\mathbf{x}^*,\mathbf{X})\left(\mathbf{K}+\sigma_{\varepsilon}^2\mathbf{I}\right)^{-1}\mathbf{y}\\ \boldsymbol{\Sigma}^* &= k(\mathbf{x}^*,\mathbf{x}^*)-k(\mathbf{x}^*,\mathbf{X})\left(\mathbf{K}+\sigma_{\varepsilon}^2\mathbf{I}\right)^{-1}k(\mathbf{X},\mathbf{x}^*) \end{align} $$
at inputs $\mathbf{x}^*$. However, to evaluate the expected return, we need to perform long-term predictions. In the case of the GP, we can use iterated moment matching1 to produce a probabilistic trajectory $[\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1, \boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2 \dots, \boldsymbol{\mu}_T, \boldsymbol{\Sigma}_T]$.
In prior work2, safety constraints are considered for trajectories of this form by reasoning about the “distance” in standard deviations between the mean of each state marginal distribution $p(\mathbf{x}_t) = \mathcal{N}(\boldsymbol{\mu}_t, \boldsymbol{\Sigma}_t)$ and the constraint bound2. For example, a hard constraint $\mathbf{x}_t < b$, is transformed into a chance constraint $p(\mathbf{x}_t < b) \geq 0.95$ where the constraint must be satisfied by all $\mathbf{x}_t$ within two standard deviations of $\mathbb{E}[\mathbf{x}_t]$.
However, this safety approach strongly relies on the assumption that the state marginal distributions $p(\mathbf{x}_t)$ are Gaussian distributed. Also, generating a trajectory (i.e., by sampling the state marginals) through $\mathbf{y}_t \sim p(\boldsymbol{\mu}_t, \boldsymbol{\Sigma}_t) ,$ for $t=1,2,\dots, T$ produces trajectories that are dynamically implausible because the repeated sampling corresponds to changing the dynamics model at every time step, which leads to a “disconnected” trajectory. Trajectories produced this way are unsafe for real-world execution.
Pathwise Trajectory Sampling
Recently, Wilson et al.3 introduced an efficient method for drawing samples from GP posteriors called Matheron’s rule for Gaussian processes $$ \begin{align} \underbrace{(f\mid \mathbf X, \mathbf y)(\cdot)}_{\text{posterior}} &\stackrel{d}{=} \underbrace{f(\cdot)}_{\text{prior}} + \underbrace{k(\cdot,\mathbf{X})(\mathbf{K} + \sigma_\varepsilon^2 \mathbf I)^{-1}(\mathbf y-f(\mathbf X))}_{\text{data-dependent update}} \end{align} $$ where we draw samples from the GP prior and add a data-dependent update term to transform them into samples from the GP posterior, resulting in a sample-based representation for the posterior. This is important for our context because each individual samples corresponds to a smooth, deterministic trajectory $f_i$ which can be evaluated at any test location $\mathbf{x}_t$. As such, the state marginal distributions $p(\mathbf{x}_t)$ are not restricted to Gaussian form. Also, trajectories are temporally correlated and thus dynamically plausible.
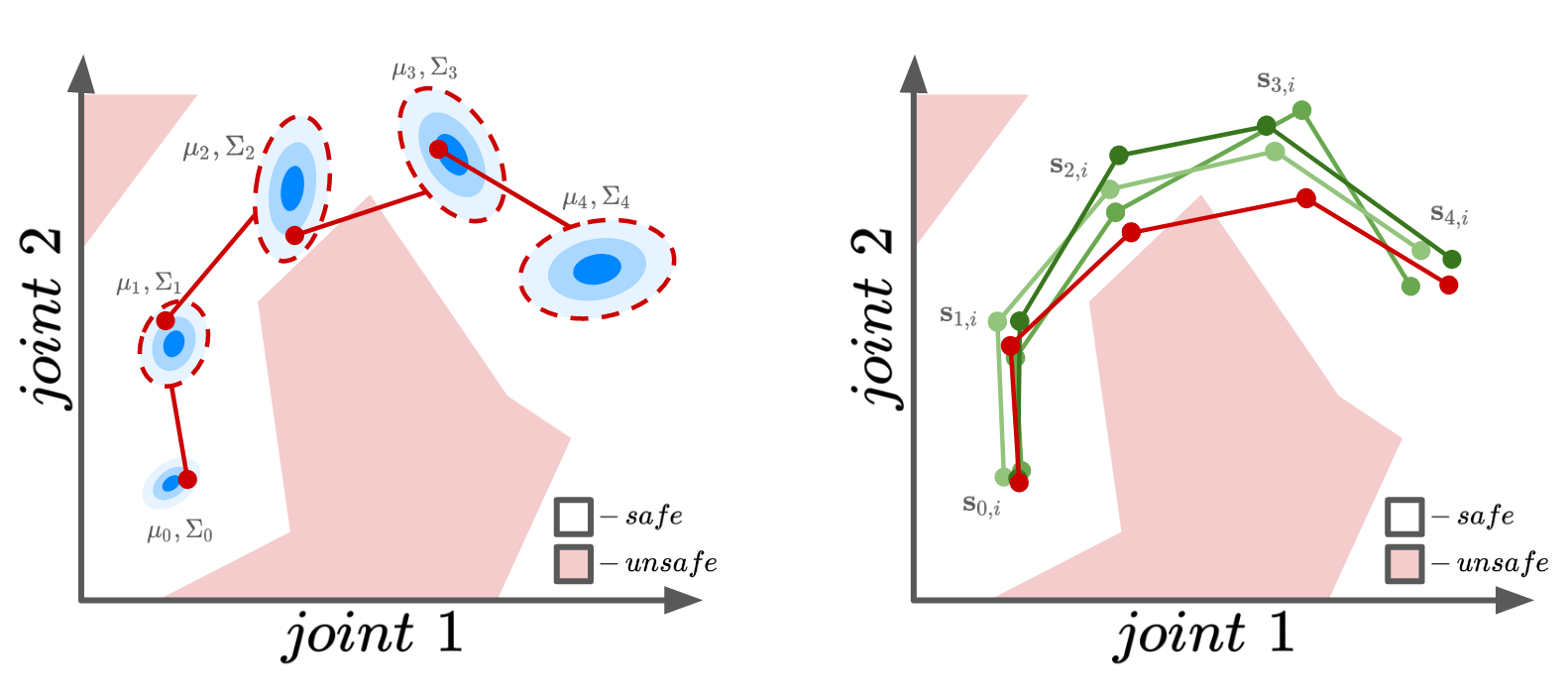
Figure 1. A comparison between probabilistic trajectories and pathwise sampled trajectories for a 2-DOF robot. While the state moment-based representation (left) may have "safe" state marginal, it is still possible to sample trajectories that violate constraints. In the pathwise approach (right), we can effortlessly tell the difference between safe and unsafe trajectories.
When paired with sparse Gaussian process approximations, this pathwise posterior sampling approach scales linearly with the number of test locations, a stark difference to the usual cubic complexity of standard Gaussian Processes. This efficiency in sampling is extremely important for reinforcement learning purposes.
Adding Safety
The additional benefit of using the sampling-based representation of the GP posterior is that we can isolate constraint-violating trajectories from safe ones.
In this work, we achieve this by performing rejection sampling on the pathwise sampled trajectories, discarding trajectories with state violations and using the remaining trajectories to estimate the expected return. In the second safety approach, we add soft constraint penalty terms to the reward function, such that the expected return is now given by
$$ J(\theta) = \mathbb{E}_{\pi_{\theta}}\left[\sum\limits_{t=0}^T \left(r(\mathbf{s}_{t})+c(\mathbf{s}_{t})\right)\right] $$where $r(\cdot)$ and $c(\cdot)$ are the reward and constraint terms respectively.
Experiments
We train a 0-mean GP dynamics model with an SE kernel, and RBF network policy. We evaluate the method with a simulated constrained reaching task on a 7-DoF robot arm. We consider a scenario where the robot arm operate in an environment with a low ceiling. Mathematically, this is represented as a barrier function on long the Z-axis of the robot’s workspace.

Using our method, we successfully learn a reaching policy that does not violate constraints at deployment time. This remains true even though we start from a state randomly sampled from a distribution as opposed to being kept fixed.

Summary
In MBRL, Gaussian processes can be used to learn accurate dynamics models for highly nonlinear robotics systems with limited data. However, the distributional representation of trajectories in this setting makes it difficult to reason about safety constraints. In this work, we propose to use a trajectory sampling approach that directly generates sample trajectories from the GP without making Gaussian assumptions on the predictive state marginals, obeys time correlations between consecutive states, and can be directly executed on the robot, as seen in Figure 1. Our safe trajectory approach consists of a convenient particle GP posterior representation3, a rejection sampling procedure, and penalty terms added to the reward function. Our experiments show that our approach can learn safe policies that are still compatible with the physical robot. If you, like us, find this work interesting, we invite you to read the full paper.
References
M. P. Deisenroth and C. E. Rasmussen. PILCO: A Model-based and Data-efficient Approach to Policy Search. ICML, 2011. ↩︎ ↩︎
S. Kamthe and M. P. Deisenroth. Data-Efficient Reinforcement Learning with Probabilistic Model Predictive Control. AISTATS, 2018. ↩︎ ↩︎
J. T. Wilson, V. Borovitskiy, A. Terenin, P. Mostowsky, and M. P. Deisenroth. Pathwise Conditioning of Gaussian Processes. JMLR, 2021. ↩︎ ↩︎